Solving the first problem: n=15 and p=0.4.
Step-by-step explanation:
Step 1. We are given the number of trials n

And the probability of success:

We need to find the probability of 4 successes P(4).
Step 2. Since it s a problem where the outcome is either success or failure, we use the binomial distribution formula:

Where p(x) is the probability of x successes. x is the number of successes, and q is the probability of a failure.
Step 3. In this case, x is 4:

The probability of failure is defined as follows:
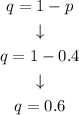
Step 4. Substituting the known values into the binomial distribution formula:
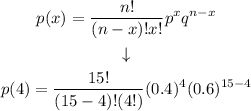
Solving the operations:

Step 5. Solving step by step and simplifying the factorial expressions, the result is:

The probability is 0.126776
Answer:
