Question

. You have budgeted $48.50 to purchase books and CD's for your toddler. Each book costs an average of$3.95 and each CD costs an average of $3.10. Because the shelf you are storing them on is only so big, youhave decided you will not purchase over 14 books and CD's combined. You are going to resell the booksand want to make a maximum profit. You will make a profit of 5$ for each book and 4$ each CD.a. Write a system of linear inequalities to find the possible amounts that can be purchased.

Answer 1

We have to write a system of inequalities to find the possible amount od CD's and books that can be purchased.

The profit function can be expressed as the sum of the profit of each piece multiplied by the number of CD's or books.

If C is the number of CD's and B is the number of books, we can write:

`P(C,B)=5B+4C`

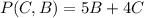
The constraints are:

- The budget, that is $48.50.

- The space in the shelf, that fits 14 items.

Then, we can write that the sum of the money spent on CD's and the money spent on books should be equal or less than $48.50:

`3.95\cdot C+3.10\cdot B\le48.50`

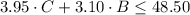
For the shelf, we can write that the sum of CD's and books is equal or less than 14:

`C+B\le14`

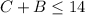
Answer:

a) The linear inequalities (constraints) for this problem are:

3.95C + 3.10B ≤ 48.50

C + B ≤ 14