Question

Mazie stands on her kitchen floor. The coefficient of kinetic friction between her socks and the floor is .62, and the coefficient of static friction is .75. She has a mass of 42 kg. A. Mazie slides across the floor at a speed of 1.3 m/s. What is the force of kinetic friction acting on her?B. Mazie climbs up on the roof of her house, which has an angle of 35°. The coefficient of static friction between her and the roof is 0.51. Will she slip off the roof?

Answer 1

A.

In order to calculate the force of kinetic friction, we can use the formula:

`F=N\cdot\mu`

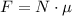
Where N is the normal force and μ is the coefficient of kinetic friction.

Since the floor is horizontal, the normal force is equal the weight, so we have:

`\begin{gathered} N=m\cdot g \\ F=m\cdot g\cdot\mu \\ F=42\cdot9.81\cdot0.62 \\ F=255.45\text{ N} \end{gathered}`

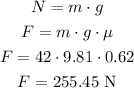
B.

First let's calculate the horizontal component of the weight:

`\begin{gathered} F_x=m\cdot g\cdot\sin (35\degree) \\ F_x=42\cdot9.81\cdot0.5736 \\ F_x=236.33\text{ N} \end{gathered}`

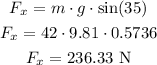
Now, let's calculate the friction force:

`\begin{gathered} N=m\cdot g\cdot\cos (35\degree) \\ F=N\cdot\mu \\ F=m\cdot g\cdot\cos (35\degree)\cdot0.51 \\ F=42\cdot9.81\cdot0.819\cdot0.51 \\ F=172.1\text{ N} \end{gathered}`

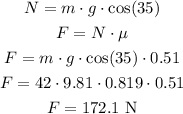
Since the horizontal compontent of the weight is greater than the friction force, she will slip off the roof.