Let a represent the cost of adult tickets and c represent the cost of children's tickets.
On the first day, $138.50 worth of tickets were sold by selling 5 adult tickets and 2 child tickets. This means that:
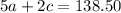
On the second day, $185.50 worth of tickets were sold by selling 7 adult tickets and 2 child tickets. This means that:
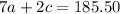
We can solve the simultaneous equations by subtracting the two equations:
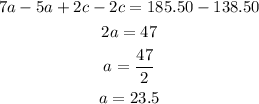
We can solve for c by substituting for a into the first equation:
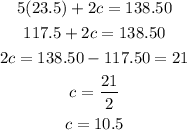
Therefore, an adult ticket costs $23.50 and a child ticket costs $10.50.