Question

o MIDSEGMENT THEOREM 12)Triangle ABC has vertices A(-5,2), B(1,5) and C(1,-1). Determine the point of intersection of the medians, and state its coordinate

Answer 1

To determine the point of intersection of the medians and its cordinate:

Let O(x, y) be the centroid of the triangle.

The median of a triangle is a line segment that joins the vertex of a triangle to the midpoint of the opposite side. There are three medians in a triangle; and the medians of a triangle intersect at a point called the centroid.

The centroid of a triangle is gotten from the average of the x coordinates and the y coordinates of all the three vertices.

For Triangle ABC has vertices A (-5,2) B (1,5) C (1,-1) and centroid O(x, y).

Hence:

`x=(-5+1+1)/(3)=-(3)/(3)=-1`
`y=(2+5+(-1))/(3)=(7-1)/(3)=(6)/(3)=2^{}`

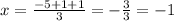
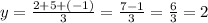
The centroid is at (-1, 2)

Hence the point of intersection and coordinate = (-1 , 2)