Question

ShopRite, a customer purchased 15 apples and 8 plums for $23.51. Another customer purchased 9 apples and 4 plums for $13.33. Write and solve a system of equations to find the cost of each apple and plum?

Answer 1

Let the cost of one apple is 'x' while the cost of a plum is 'y'.

Given that a customer purchased 15 apples and 8 plums for $23.51,

Since an apple costs x , the cost of 15 apples is 15 times x, that is 15x. Similarly the cost of 8 plums is 8 times y that is 8y. Now the total cost of making the purchase must be equal to $23.51,

`15x+8y=23.51`

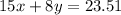
Given that another customer purchased 9 apples and 4 plums for $13.33.

Since an apple costs x , the cost of 9 apples is 9 times x, that is 9x. Similarly the cost of 4 plums is 4 times y that is 4y. Now the total cost of making the purchase must be equal to $13.33,

`9x+4y=13.33`

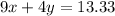
Solve the given equations using Elimination Method.

Mutiply the second equation by (-2) and add it to the first equation,

`-2(9x+4y)+(15x+8y)=-2(13.33)+23.51\Rightarrow-18x-8y+15x+8y=-26.66+23.51`

`-3x+0=-3.15\Rightarrow x=(-3.15)/(-3)\Rightarrow x=1.05`

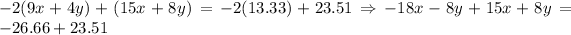
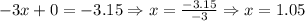
Substitute this value in the first equation to obtain the value of 'y'.

`15(1.05)+8y=23.51\Rightarrow8y=23.51-15.75\Rightarrow y=(7.76)/(8)\Rightarrow y=0.97`

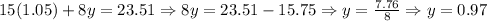
The obtained values of x and y are 1.05 and 0.97 respectively.

Thus, the cost of each apple is $1.05 and that of each plum is $0.97.