Question

1/2 60 degrees, 30 degrees find x and y

Answer 1

We will investigate the application of trignometric ratios.

There are three trigonometric ratios that are applied with respect to any angle in a right angle triangle as follows:

`\begin{gathered} \sin \text{ ( }\theta\text{ ) = }(P)/(H) \\ \\ \cos \text{ ( }\theta\text{ ) = }(B)/(H) \\ \\ \tan \text{ ( }\theta\text{ ) = }(P)/(B) \end{gathered}`

Where,

`\begin{gathered} \theta\colon\text{ Any of the chosen angle of a right angle traingle except ( 90 degrees )} \\ P\colon\text{ Side opposite to the chosen angle} \\ B\colon\text{ Side adjacent/base to chosen angle} \\ H\colon\text{ Hypotenuse} \end{gathered}`

We have two options to select our angle theta from:

`\theta=\text{ 60 OR }\theta\text{ = 30}`

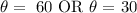
We can choose either of the above angles. We will choose ( 30 degrees ); hence:

`\begin{gathered} \theta\text{ = 30} \\ P\text{ = }(1)/(2)\text{ , B = y , H = x} \end{gathered}`

We will use the trigonmetric ratios and evaluate each of the variables ( x and y ).

To determine ( x ) we can use the sine ratio as we have ( P ) and ( theta ) we can evaluate the hypotenuse as follows:

`\begin{gathered} \sin (30)\text{ = }((1)/(2))/(x) \\ \\ x\text{ = }((1)/(2))/((1)/(2)) \\ \\ x\text{ = 1}\ldots\text{Answer} \end{gathered}`

To determine ( y ) we can use the tangent ratio as we have ( P ) and ( theta ) we can evaluate the Adjacent/base side as follows:

`\begin{gathered} \tan (30)\text{ = }((1)/(2))/(y) \\ \\ y\text{ = }\frac{(1)/(2)}{\frac{\sqrt[]{3}}{3}} \\ \\ y\text{ = }\frac{1}{2\cdot\sqrt[]{3}}\ldots\text{Answer} \end{gathered}`