We have the Word COCONUT and the word CHOCOLATE as we can see the common letter in the word are C, O, T
The probability to obtain a letter that in the word Chocolate is
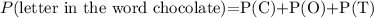
where
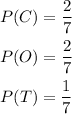
then we substitute this information
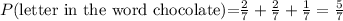
The probability to chose a card that it will be a letter in the word CHOCOLATE is 5/7