Question

Help I don’t understand and my last tutor didn’t even answer the problem

Answer 1

Area and Definite Integrals

Definite integrals can be used to find the area under the graph of the functions and the x-axis. But integrals compute the areas above the x-axis as positive and below the x-axis as negative, so if we want to calculate the unsigned area, we must take care of the sign of the function in the given interval.

We are given the function:

`f(x)=5-5x^2`

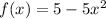
And it's required to calculate the area between the x-axis and the function in the interval [0, 5]. We must find out if the graph crosses the x-axis to account for the change of signs.

To find possible roots of the function, we equate to zero:

`\begin{gathered} 5-5x^2=0 \\ \text{Divide by -5:} \\ -1+x^2=0 \\ Add\text{ 1:} \\ x^2=1 \\ x=\sqrt[]{1}=\pm1 \end{gathered}`

The root x = 1 belongs to the interval [0,5], thus the function changes signs at that point. An approximate graph of the function is shown below:

We can see the function is positive before x = 1 and negative after x = 1, so the integral for the last part should have the sign inverted as follows:

`A=\int ^1_0(5-5x^2)dx-\int ^5_1(5-5x^2)dx`

Calculate the indefinite integral:

`\begin{gathered} I=\int ^{}_{}(5-5x^2)dx \\ I=5x-(5)/(3)x^3 \end{gathered}`

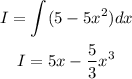
Calculate the first integral evaluating it in 0 and 1:

`\begin{gathered} (5\cdot1-(5)/(3)1^3)-(5\cdot0-(5)/(3)0^3) \\ 5-(5)/(3)=(10)/(3) \end{gathered}`

Evaluate the second integral for x = 1 and x = 5:

`\begin{gathered} (5\cdot5-(5)/(3)5^3)-(10)/(3) \\ (25-(625)/(3))-(10)/(3) \\ -(560)/(3) \end{gathered}`

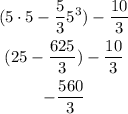
The required area is:

`A=(10)/(3)+(560)/(3)=(570)/(3)=190`

The area is 190 square units