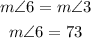Answer:
• m∠2 = 90°
,
• m∠3 = 73°
,
• m∠4 = 17°
,
• m∠5 = 90°
,
• m∠6 = 73°
Step-by-step explanation:
Angle 2 is a right angle, therefore:
• m∠2 = 90°
Given that m∠1 = 17°:
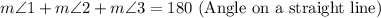
Substitute the given values:
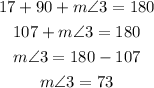
• m∠3 = 73°
Angles 1 and 4 are vertically opposite angles, therefore:
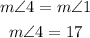
Angles 2 and 5 are vertically opposite angles, therefore:
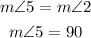
Angles 3 and 6 are vertically opposite angles, therefore: