The Solution.
An Algebraic Equation can be defined as a mathematical statement that involves the following:
i. At least a letter ( an unknown)
ii. At least a number
iii. And an equality sign (i.e =)
An algebraic equation can be presented in any of the following ways without changing its meaning:
1. When you interchange an equation. For example, supoose the original equation is 2y+1 =6, when interchanged we get, 6=2y+1
So, 2y+1=6 has the same meaning as 6=2y+1
2. When you multiply through an initial equation by a positive or negative quantity( that is, mltiply both sides by a quantity). For example,
2y+1=6 has the same meaning as 2(2y+1)=2(6)
3. When you divide both sides of an equation by a quantity, the initial equation remain unchanged. For example,
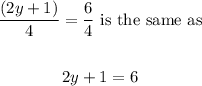
4. If you add or subtract same quantity from both sides, the initial equation still remains the same. For example,
