We have to determine wheter the line segments MN and RS are parallel, perpendicular or neither. To do this we will find the slope of each of this segments; the slope is given by

For the line segment MN we have M(-2,2) and N(1,-3), then
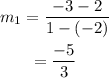
For the line segment RS we have R(-2,1) and (3,4), then
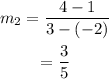
Now that we have the slopes of each lines segments we have to remember two theorems.
T1. Two lines are parallel if and only if
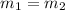
T2. Two lines are perpendicular if and only if
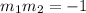
Once we know this theorems we can answer the question.
First, we notice that the slopes of this segments are not equal so we can conlcude that they are not parallel.
Let's see if they are perpendicular, to do this we multiply the slopes
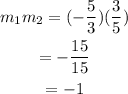
Since the result of their multiplication is -1 we conclude that this lines segments are perpendicular.