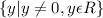The function is given as
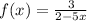
To find the inverse of the function, replace x with y.
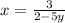
Now solve for y.
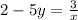
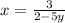
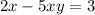
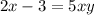
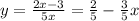
Thus the inverse of the function is
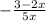
Now to find the domain of the function is
The domain of the function is the set of values of x for which the function is defined.
The domain of the inverse function is
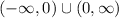
Hence the correct option is B.