Question

Suppose you need average speed of 100 km/h to arrive at a certain destination on time. However, trafficlimits your average speed to only 60 km/h during the first half of the trip's distance. What must youraverage speed be in the second half of the trip to be on time?

Answer 1

140 km/h

Step-by-step explanation:

If you have a speed of v1 the first half of the trip and a speed of v2, the second half of the speed, the average speed will be

`v_{\text{avg}}=(v_1+v_2)/(2)`

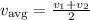
Solving for v2, we get:

`\begin{gathered} 2v_{\text{avg}}=v_1+v_2 \\ 2v_{\text{avg}}-v_1=v_2 \\ v_2=2v_{\text{avg}}-v_1 \end{gathered}`

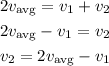
Then, we can replace the average speed Vavg = 100 km/h and the speed of the first half v by 60 km/h

Therefore, the speed in the second half of the trip must be 140 km/h