Question

Evaluate the expression: 9² × 2 - 4²2 × (10-2) ÷ 2²30 - (3³ - 8)

Answer 1

We have to evaluate the expressions.

We have to solve each operation in the correct order: first the operations within the parenthesis, and within them, first the powers, then the multiplication/quotients and lastly the adds/subtractions. Then, we apply the same sequence for the terms outside the parenthesis.

a)

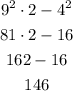
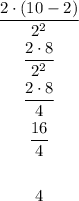
`\begin{gathered} 9^2\cdot2-4^2 \\ 81\cdot2-16 \\ 162-16 \\ 146 \end{gathered}`

b)

`\begin{gathered} (2\cdot(10-2))/(2^2) \\ (2\cdot8)/(2^2) \\ (2\cdot8)/(4) \\ (16)/(4) \\ \\ 4 \end{gathered}`

c)

`\begin{gathered} 30-(3^2-8) \\ 30-(9-8) \\ 30-1 \\ 29 \end{gathered}`

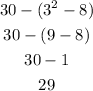
Answer: a) 146, b) 4 c) 29