Question

Which of the following best describes the figure with vertices (-8, 2), (4, 14), (16, 2) and(4, -10)? thank

Answer 1

Given:

Vertices (-8, 2), (4, 14), (16, 2) and (4, -10).

Required:

To find the figure that is made by the vertices.

Step-by-step explanation:

Let A (-8, 2), B(4, 14), C(16, 2) and D(4, -10).

Then find the length of each side by using the distance formula.

`\begin{gathered} AB=√((4+8)^2+(14-2)^2) \\ AB=√((12)^2+(12)^2) \\ AB=√(144+144) \\ AB=12√(2) \end{gathered}`
`\begin{gathered} BC=√((16-4)^2+(2-14)^2) \\ BC=√((12)^2+(-12)^2) \\ BC=√(144+144) \\ BC=12√(2) \end{gathered}`
`\begin{gathered} CD=√((4-16)^2+(-10-2)^2) \\ CD=√((-12)^2+(-12)^2)^ \\ CD=√(144+144) \\ CD=12√(2) \end{gathered}`

`\begin{gathered} AD=√((4+8)^2+(-10-2)^2) \\ AD=√((12)^2+(-12)^2) \\ AD=√(144+144) \\ AD=12√(2) \end{gathered}`

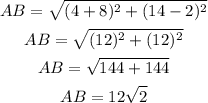
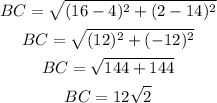
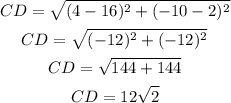
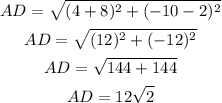
All sides are equal.

AB =BC = CD = AD

We know that the figure in which all sides are equal is called a square.

Final Answer:

Option 2 is the correct answer.