Question

Petunia has a vegetable garden and has collected data about the amount of rain received and how high her tomato plant is growing. She displayed the information as graphed below.Based on the trend line, how tall should her tomato plant grow if there is 11 cm of rain? A. 9 cm B. 11 cm C. 10 cm D. 8 cm

Answer 1

To get the solution to the problem, we will need to get the relationship in terms of an equation in the linear form given to be:

`y=mx+b`

where m is the slope, b is the y-intercept, y is the height of tomato, and x is the amount of rain.

The slope can be calculated using the formula:

`m=(y_2-y_1)/(x_2-x_1)`

From the diagram, we can get two points as sown below:

Therefore, the slope will be:

`\begin{gathered} (x_1y_1)=(0,0) \\ (x_2,y_2)=(6,5) \\ \therefore \\ m=(5-0)/(6-0)=(5)/(6) \end{gathered}`

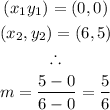
The y-intercept is b = 0.

Therefore, the equation becomes:

`y=(5)/(6)x`

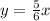
Therefore, for 11 cm of rain, the