The external angle is suplementary to the internal angle close to it. We also know that the sum of all the internal angles of the triangle are equal to 180 degrees, this means that the angle "a" is suplementary to the sum of the angles "b" and "c". Through this logic, we can conclude that since:
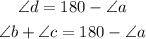
Then we can conclude that:
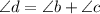
Therefore the statement is true, the exterior angle is equal to the sum of its remote interior angles.
Let's use an example:
On this example, the external angle is 120 degrees, therefore the sum of the remote interior angles must also be equal to that. Let's try:
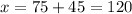
The sum of the remote interior angles is equal to the external angle.