Answer:
A) 30.6%
B) 420,500 batteries
Explanations:
A) First, we need to convert the range of number of hours to z-scores, this can be expressed as:
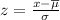
where
µ is the mean value
σ is the standard deviation
If the number of hours is 4120 hours, then the z-score will be;
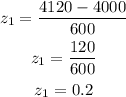
If the number of hour is 4720 hours, then the z-score wil be;
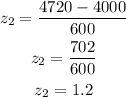
The equivalent z-score will be;
![0.2Find the equivalent probability[tex]\begin{gathered} P(0.2Hence the <strong>percentage of batteries</strong> that will last between 4120 and 4720 hours is <strong>30.6%</strong><p></p><p>B) In order to determine the total batteries that will<strong> last up to 4600 hours</strong> if the there are<strong> 500,000 batteries</strong>, we will have;</p>[tex]\begin{gathered} z=(4600-4000)/(600) \\ z=(600)/(600) \\ z=1 \end{gathered}]()
Such that;

Find the required number of batteries
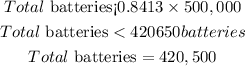
Since 420,500 is less than the calculated, hence the total batteries that will last up to 4600 hours is 420,500 batteries