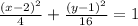The general equation of an ellipse is
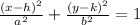
Where (h, k) are the coordinates of the center.
For our ellipse, we already have the center (2, 1), then, our equation will be
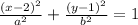
Using the points that belong to this ellipse, we can substitute them on this equation to find the coefficients a and b.
First, let's use the point (4, 1). Doing the substitution, we have
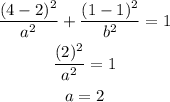
Using the other point, we can calculate the other coefficient.
![\begin{gathered} ((1-2)^2)/(4)+\frac{(1+2\sqrt[]{3}-1)^2}{b^2}=1 \\ ((-1)^2)/(4)+\frac{(2\sqrt[]{3})^2}{b^2}=1 \\ (1)/(4)+\frac{12^{}}{b^2}=1 \\ \frac{12^{}}{b^2}=(3)/(4) \\ 4\cdot12=3\cdot b^2 \\ b^2=16 \\ b=4 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/rbhjhrflu3av9yft306de7pc21zbd95alj.png)
And then, we have our ellipse equation.