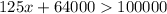Question

A charity is trying to raise $200,000 by holding a benefit concert. The charity's volunteers have already raised $64,000 from ticket sales, and each ticket sold brings the volunteers $125 closer to their goal. The lead volunteer wants to figure out how many more tickets must be sold until they will have raised more than half of their goal.This problem can be solved with an inequality that uses the variable X.Which inequality can be used to solve this problem?1) 125x-100,000 > 640002) 125x >= 100,0003) 125x + 64000 >= 2000004) 125x + 64000 > 100,000

Answer 1

Given that a Charity is trying to raise $200,000 by holding a benefit concert, and the volunteers have raised $64,000 from ticket sales.

Each ticket sold brings the Volunteers $125 closer to their goal.

To determine how many ticket must be sold until more than half their goal is raised,

let x represent the amount of tickets the volunteers still need to sell.

For the volunteers to raise more than half their goal,

Half their goal:

`\begin{gathered} (1)/(2)*\$\text{200000=} \\ =\$100000 \end{gathered}`

Since x represent the amount of tickets the volunteers need to sell, the amount closer to the goal is thus

`\begin{gathered} \$125* x \\ =\$125x \end{gathered}`

Since the Volunteers have already $64,000, thus we have

`\begin{gathered} amount\text{ raised > half the goal} \\ (64000+125x)>100000 \end{gathered}`

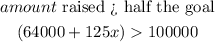
Hence, we have the inequality to be

`125x+64000>100000`