Question

Hi, can you help me answer this question, please, thank you:)

Answer 1

If the number of tablets in a shipment is sufficiently large, we can consider the testing procedure you describe (selecting a random sample of 21 ibuprofen tablets and counting the number of defective tablets in the sample) to be a binomial probability experiment.

Let X = (Number of defective ibuprofen tablets in a random sample of 21 tablets.) Then we may reasonably assume that X follows a binomial distribution. For each "trial" (that is, each tablet selected), there are two possible outcomes, "success" (the tablet is defective), or "failure" (the tablet is not defective).

Note that the word success as used in the binomial distribution does not carry the connotation of being a "good" outcome. A "success" is simply the outcome you are interested in counting, which in this case is the number of defectives in the sample.

The important parameters for a binomial distribution are n (the number of trials) and p (the probability of success on any one trial.)

For this situation, we have p= 0.01 (since we are told 1% of the tablets in the shipment are defective) and n = 21.

The general formula for the binomial distribution is

`P(x)=^nC_xp^x(1-p)^(n-x)`

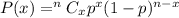
Where x is the number of successes in n trials (In this problem, x is the number of defectives in a random sample of 21 tablets.)

The symbol nCx is the "number of combinations of n things taken x at a time". This is the number ways of choosing x distinct objects from a set of n objects, without regard to order.

It is given by

`^nC_x=(n!)/(x!(n-x)!)`

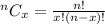
where ! is the factorial symbol.

We want to find the probability that the shipment is accepted. We are told that a shipment will be accepted if at most one tablet doesn't meet the required specifications. That is, the number of defectives must be less than or equal to one.

P(Shipment accepted) = P(x ≤ 1). (In this case, x ≤ 1 if and only if x=0 or x=1) =P(0) + P(1)

So we calculate P(0) (the probability of 0 defective tablets in the shipment),

and P(1) (the probability of 1 defective.)

Using the formula for the binomial distribution, we have

`\begin{gathered} P(0)=^(21)C_0(0.01)^0(1-0.01)^(21-0) \\ P(0)=(21!)/(0!(21-0)!)*1*0.99^(21) \end{gathered}`
`\begin{gathered} P(0)=(21!)/(1*21!)*1*0.809728 \\ P(0)=1*1*0.809728 \\ P(0)=0.809728 \end{gathered}`
`\begin{gathered} P(1)=^(21)C_1(0.01)^1(1-0.01)^(21-1) \\ P(1)=(21!)/(1!(21-1)!)*0.01*0.99^(20) \end{gathered}`
`\begin{gathered} P(1)=(21!)/(1*20!)*0.01*0.817907 \\ P(1)=(21*20!)/(20!)*0.01*0.817907 \\ P(1)=21*0.00817907 \\ P(1)=0.171760 \end{gathered}`

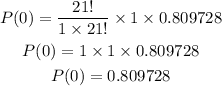
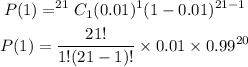
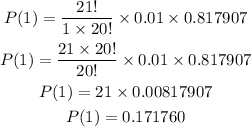
Finally, then, we have:

P(Shipment accepted)= P(0) + P(1)

`\begin{gathered} P(0,1)=0.809728+0.171760 \\ P(0,1)=0.981488 \\ P(0,1)\approx0.9815(4decimal\text{ place)} \end{gathered}`

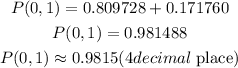
Hence, the probability that this whole shipment will be accepted if a particular shipment of thousands of ibuprofen tablets actually has a 1% rate of defects is 0.9815 corrected to 4 decimal places