The equation of a circle located at a distance (a,b) from the origin is given by
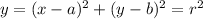
Given:

To get the coordinates, we will have to compare the given equation to the equation of the
circle
Upon comparing the terms and coefficient,
a = 6
b= 2
r = 9
Hence the center of the circle is (6,2)
radius = 9