Question

Assume that a softball player has a 0.410 batting average. Assume that this means the player has a 0.41 probability of getting a hit in each at bat. Assume that the player bats four times. What is the probability that she gets exactly two hits?Decimal rounded to four places as needed.

Answer 1

P = 0.3511

Step-by-step explanation:

Using the equation for the binomial distribution, we get that the probability can be calculated as:

`P(x)=\text{nCx}\cdot p^x\cdot(1-p)^(n-x)`

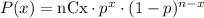
Where nCx is calculated as:

`\text{nCx =}(n!)/(x!(n-x)!)`

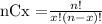
So, n is the total number of bats, x is the number of hits and p is the probability of getting a hit. So, replacing n = 4, x = 2 and p = 0.41, we get:

`\begin{gathered} 4C2=(4!)/(2!(4-2)!)=\frac{4!}{2!^{}\cdot2!}=6 \\ P(2)=4C2\cdot(0.41)^2\cdot(1-0.41)^(4-2) \\ P(2)=6\cdot(0.41)^2\cdot(0.59)^2 \\ P(2)=0.3511 \end{gathered}`

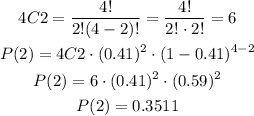
Therefore, the answer is P = 0.3511