Question

At a fabric store, fabrics are sold by the yard. A dressmaker spent $36.35 on 4.25 yards of silk and cotton fabrics for a dress. Silk is $16.90 per yard and cotton is $4 per yard. Here is a system of equations that represent the constraints in the situation. x +y = 4.25 16.90x + 4y=36.35 What does the solution to the system represent?

Answer 1

Let the number of silk be

`=x`

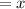
Let the number of cottons be

`=y`

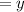
The total number of silk and cotton is 4.25 yards and this can be represented as

`=x+y=4.25\ldots\ldots\text{.}\mathrm{}(1)`

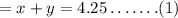
Silk is $16.90 per yard and cotton is $4 per yard has a total of $36.35

`16.90x+4y=$36.35$\ldots\ldots\ldots(2)`

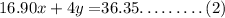
From equation one, we can get an equation 3 which will be used to solve simultaneously

`\begin{gathered} x+y=4.25 \\ y=4.25-x\ldots\ldots(3) \end{gathered}`

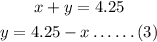
Using substitution method, substitute equation (3) in equation (2)

`\begin{gathered} 16.90x+4y=$36.35$ \\ 16.90x+4(4.25-x)=$36.35$ \\ 16.90x+17-4x=36.35 \\ \end{gathered}`

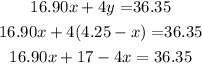
Collect similar terms

`\begin{gathered} 16.90x+17-4x=36.35 \\ 16.90x-4x=36.35-17 \\ 12.90x=19.35 \\ \text{divide both sides by 12.90} \\ (12.90x)/(12.90)=(19.35)/(12.90) \\ x=1.5 \end{gathered}`

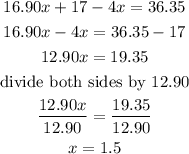
Substitute x= 1.5 in eqaution (3)

`\begin{gathered} y=4.25-x \\ y=4.25-1.5 \\ y=2.75 \end{gathered}`

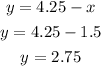
Alternatively,

Using the graphical method, we will have

Therefore,

The value of x = 1.5 , the value of y = 2.75