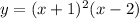Ok, we need to find a suitable equation for that graph and write it in factored formed. With this information what we can imply is that said equation is a polynomial one:

Where the r terms are the roots or zeros of the function which are the x-values for which y=0. In a graph these points correspond to the x-intercepts. In this case we have two x-intercepts which means that we have two different roots:
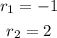
Now as stated in the factored formula I wrote before the terms (x-r) have exponents A and B. To find those exponents you'll need to use the graph. If in a x-intercept the graph of the function changes its sign then the exponent of that root is an odd number. If the sign stays the same then the exponent of that root is an even number.
The function pass from negative to positive values in x=2 so for that root the exponent is an odd number (we are gonna use 1):

In the other x-intercept, x=-1, the function is negative at both sides of that point so its exponent has to be an even number (we are gonna use 2):
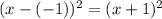
So now we have that:
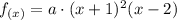
We just need to find the value of a. If you look at the graph you can see that it has a y-intercept in y=-2. This means that:
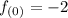
So:
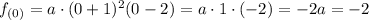
Then:
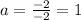
So the final factored form of the equation is: