Question

7 Given the equation below determine and state the center and radius of its circle.(x-5)² + (y + 4)² = 36

Answer 1

Given: The equation a circle below

`(x-5)^2+(y+4)^2=36`

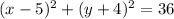
To Determine: The center and the radius

Solution

The general equation a circle given the center and the radius is

`\begin{gathered} (x-h)^2+(y-k)^2=r^2 \\ Where \\ center=(h,k) \\ radius=r \end{gathered}`

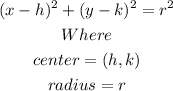
Compare the given to the general equation to get the center and radius

`\begin{gathered} (x-5)^2+(y+4)^2=36 \\ (x-5)^2+(y-(-4))^2=6^2 \\ (x-h)^2+(y-k)^2=r^2 \\ h=5,k=-4,r=6 \end{gathered}`

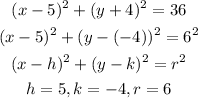
Hence, the center is (5, - 4), and radius is 6 units