Given the equation:
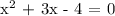
To find x, since the equation is in the standard form of Quadratic Equation, we will be using the Quadratic formula:
![\text{ x =}\frac{-b\text{ }\pm\text{ }\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/2023/formulas/mathematics/college/3levc1qi2thuvli7txr2zo6xutu46ahxv7.png)
At,
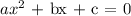
Where,
a = coefficient at x² = 1
b = coefficient at x = 3
c = constant = -4
Let's plug in the values to find for x:
![\text{ x =}\frac{-b\text{ }\pm\text{ }\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/2023/formulas/mathematics/college/3levc1qi2thuvli7txr2zo6xutu46ahxv7.png)
![undefined]()