Question

The solution to equation is
`3 ((x - 6))/(5) = x`

Answer 1

Solution of an equation

Initial explanation

We want to find which value must have x, so this equations is true:

`(3(x-6))/(5)=x`

In order to solve the equation for x we want to "leave it alone" on one side of the equation.

In order to do that we just have to remember one simple rule:

Step by step

Step 1: simplifying the expression with parenthesis

We use the distributive property to "take off" the parenthesis of the left side:

`\begin{gathered} (3(x-6))/(5)=x \\ \downarrow \\ (3x-3\cdot6)/(5)=(3x-18)/(5) \\ \downarrow \\ (3x-18)/(5)=x \end{gathered}`

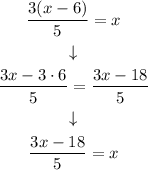
Step 2: simplifying the fraction

We take the denominator of the left to the right side:

`\begin{gathered} (3x-18)/(5)=x \\ \downarrow \\ 5\cdot(3x-18)/(5)=5\cdot x \\ \downarrow \\ 3x-18=5x \end{gathered}`

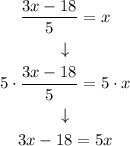
Step 3: taking all the terms with x to the right side

We take 3x to the right side:

`\begin{gathered} 3x-18=5x \\ \downarrow \\ -3x+3x-18=-3x+5x \\ \downarrow\text{ since -3x + 3x = 0 and -3x + 5x = 2x} \\ 0-18=2x \\ \downarrow \\ -18=2x \end{gathered}`

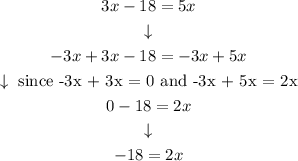
Step 4: "leaving x alone"

We take 2 to the left side:

`\begin{gathered} -18=2x \\ \downarrow \\ -(18)/(2)=(2x)/(2) \\ \downarrow\text{ since -18/2=9 and 2x/2=x} \\ -9=x \end{gathered}`

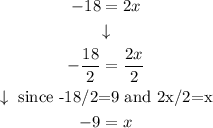
Answer: x = -9