Analyze the existence of the following limit:
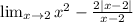
To better analyze the limit, we'll use some properties to isolate the required part from the others:
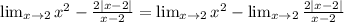
The first limit is easy to calculate, it's just to replace the value of x. The second limit will be further worked on:
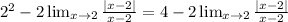
Now focus on this part:
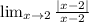
We'll approach the value of x=2 by using the set
X={-0.03, -0.02, -0.01, 0, 0.01, 0.02, 0.03}
Note these values are the infinitesimal approaches to the required value of x=2, thus the values of x to use are x={1.97, 1.98, 1.99, 2, 2.01, 2.02, 2.03}
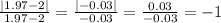
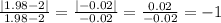
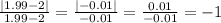
The value of x=2 cannot be used because it would produce the division 0/0 and it's undefined.
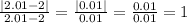
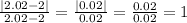
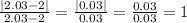
We can see this limit results in -1 for the negative values of X and 1 for the positive values of X. Since the limits are not equal, the limit does not exist