End behavior of a polynomial
In order to find the end behavior of a polynomial we simply must observe the higher exponential behavior. Since it is so much higher than the others terms it will indicate the end behavior of the total function.
In the case:
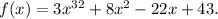
It is enough to analyze the end behavior of 3x³² in order to find the end behavior of the whole polynomial.
When x tends to infinity
When x tends to infinity
x ⇒ ∞
then
3x³² grows and grows (infinitely!)
3x³² ⇒ ∞
When x tends to minus infinity
When x tends to minus infinity
x ⇒ -∞
x takes negative numbers however x³² is always positive, because it has an even exponent, then
when x ⇒ -∞
then
3x³² grows and grows (infinitely too)
3x³² ⇒ ∞
Answer- as x ⇒ -∞, 3x³² ⇒ ∞ and as x ⇒ ∞, 3x³² ⇒ ∞