To be able to get the probability of a certain value to be selected, we need to convert it to a z-score or z-value. To convert that, we have the formula below:
![z=\frac{\bar{x}-\mu}{\frac{\sigma}{\sqrt[]{n}}}](https://img.qammunity.org/2023/formulas/mathematics/college/bqefrfb5c4zhs0vjts5lgjs1kij7yne2zk.png)
where:
bar x = sample mean
μ = population mean = 29
σ = population standard deviation = 25
n = sample size = 100
So, let's start determining the probabilities between 22.1 and 26.8 mean values.
x = 22.1
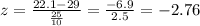
x = 26.8
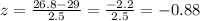
Let's plot these values to the normal curve with their corresponding areas. The corresponding areas can be found using the Z Normal Distribution.
As you can see in the graph above, the area covered from 0 to -0.88 is 0.3106 while the area covered from 0 to -2.76 is 0.4971.
To get the area covered from -0.88 to -2.76, we need to subtract the two.

Therefore, the area covered between x = 22.1 and x = 26.8 is approximately 0.187.
How to Use the Z-Table:
The above picture shows the area from 0 to 0.88. We have 0.8 as our row and 0.08 as our column. The intersection of this row and column is our area for 0.88 from the center of our normal curve. In this case, we have 0.3106.
Another example: The area to the left of -0.32 or z ≤ -0.32.
In the figure above, the area to the left of -0.32 is the one colored in green. The red area is the area from -0.32 to the center 0 which is 0.1255.
Remember, the area from the center of the normal curve is 0.5. If the red area is already 0.1255, how much is left for the green area?
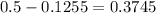
Therefore, the area to the left of z = -0.32 is 0.3745 or 0.375.