Answer:
The parent function of the function represented in the table is exponential
If function f is vertically compressed by a factor of 1/4, the f(x) - values will be divided by 4.
A point in the table for the transformed function is (1, 6)
Step-by-step explanation:
The x values are increasing by 1 unit at a time, but the f(x) is always half the value before, for example
96/2 = 48
48/2 = 24
24/2 = 12
12/2 = 6
This is the behavior of an exponential function and the equation that describes this table is:
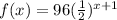
Because
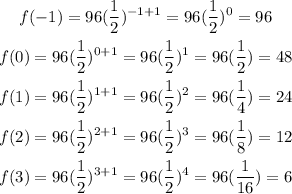
Therefore, the parent function represented in the table is Exponential.
Then, to make a vertical compression by a factor of 1/4, we need to multiply the values of f(x) by 1/4. It is the same to divide the values of f(x) by 4.
So, if function f is vertically compressed by a factor of 1/4, the f(x) - values will be divided by 4.
Therefore, the equation for the vertical compressed function is:
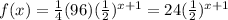
So, we can verify that (1, 6) is a point in the transformed function by replacing x by 1 on the equation above.
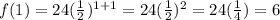
Then, a point in the table for the transformed function is (1, 6)