Notice that if we expand the product for the function R(x), we obtain a quadratic equation:
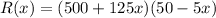
The graph of a quadratic function is a parabola, and the x-coordinate of the vertex of the parabola is located between the zeros of the function.
The zeros of the function are given by the equations:
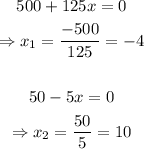
Then, the x-coordinate of the vertex of the parabola is:
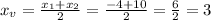
For x=3, the price of the yearbooks is:
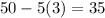
The possible maximum revenue would be:
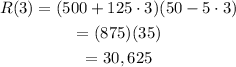
And the amount of yearbooks they would sell is:
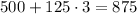
Therefore, the answers are:
Price of the yearbooks: $35
Maximum possible revenue: $30,625
Amount of yearbooks they will sell: 875