Question

I need to know what the value would be for each one.

Answer 1

Notice that if we expand the product for the function R(x), we obtain a quadratic equation:

`R(x)=(500+125x)(50-5x)`

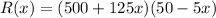
The graph of a quadratic function is a parabola, and the x-coordinate of the vertex of the parabola is located between the zeros of the function.

The zeros of the function are given by the equations:

`\begin{gathered} 500+125x=0 \\ \Rightarrow x_1=(-500)/(125)=-4 \\ \\ 50-5x=0 \\ \Rightarrow x_2=(50)/(5)=10 \end{gathered}`

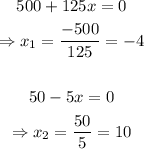
Then, the x-coordinate of the vertex of the parabola is:

`x_v=(x_1+x_2)/(2)=(-4+10)/(2)=(6)/(2)=3`

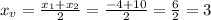
For x=3, the price of the yearbooks is:

`50-5(3)=35`

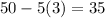
The possible maximum revenue would be:

`\begin{gathered} R(3)=(500+125\cdot3)(50-5\cdot3) \\ =(875)(35) \\ =30,625 \end{gathered}`

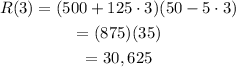
And the amount of yearbooks they would sell is:

`500+125\cdot3=875`

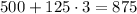
Therefore, the answers are:

Price of the yearbooks: $35

Maximum possible revenue: $30,625

Amount of yearbooks they will sell: 875