Question

Write the equation of the line perpendicular to y = 4x+7 that passes through the point (-3,5).

Answer 1

In general, if two lines are perpendicular, the product of their slopes is equal to -1. Let m be the slope of the line we are trying to find, notice that the slope of the given line is 4; therefore,

`\begin{gathered} m\cdot4=-1 \\ \Rightarrow m=-(1)/(4) \end{gathered}`

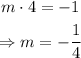
The equation of the line we need to find is -1/4.

Given the slope and a point on a line, we can find the equation of such line using the formula below

`\begin{gathered} (x_1,y_1)\to\text{ point on the line} \\ m\to\text{slope of the line} \\ y-y_1=m(x-x_1) \end{gathered}`

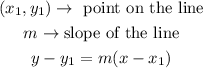
In our case,

`\begin{gathered} (-3,5),m=-(1)/(4) \\ \Rightarrow y-5=-(1)/(4)(x-(-3)) \\ \Rightarrow y-5=-(1)/(4)(x+3) \\ \Rightarrow y-5=-(1)/(4)x-(3)/(4) \\ \Rightarrow y=-(1)/(4)x+(17)/(4) \end{gathered}`

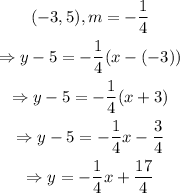
The answer is y=-x/4+17/4