Question

A researcher compares the effectiveness of two different instructional methods for teaching pharmacology. A sample of 51 students using Method 1 produces a testing average of 81.6. A sample of 76 students using Method 2 produces a testing average of 76.4. Assume the standard deviation is known to be 12.24 for Method 1 and 11.19 for Method 2. Determine the 90% confidence interval for the true difference between testing averages for students using Method 1 and students using Method 2. Step 2 of 2 : Construct the 90% confidence interval. Round your answers to one decimal place g.

Answer 1

90% confidence interval is: ( 1.7 to 8.7 )

Explanation:

Given the data in the question;

Method 1 Method 2

n₁ = 51 n₂ = 76

x"₁ = 81.6 x"₂ = 76.4

σ₁ = 12.24 σ₂ = 11.19

Lets get the Margin of Error(M.E)

M.E =
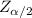`Z_{\alpha /2` √(σ₁²/n₁ + σ₂²/n₂ )

for 90% confidence interval

∝ = 1 - 0.90 = 0.10

∝/2 = 0.10/2 = 0.05

`Z_{\alpha /2` =
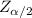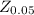`Z_{0.05` = 1.64

so we substitute

M.E = 1.64 × √((12.24)²/51 + (11.19)²/75 )

M.E = 1.64 × √( 2.9376 + 1.669548)

M.E = 1.64 × √( 2.9376 + 1.669548)

M.E = 3.52

so, for 90% confidence interval for x"₁ - x"₂ will be;

C.I = x"₁ - x"₂ ±
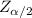`Z_{\alpha /2` √(σ₁²/n₁ + σ₂²/n₂ )

= 81.6 - 76.4 ± M.E

= 81.6 - 76.4 ± 3.52

= 5.2 ± 3.52

Lower Limit = 5.2 - 3.52 = 1.68 ≈ 1.7

Upper Limit = 5.2 + 3.52 = 8.72 ≈ 8.7

Therefore; 90% confidence interval is: ( 1.7 to 8.7 )