Question

The area A, in square meters, of a rectangle with a perimeter of 80 meters is given by the equation A = 40w − w2, where w is the width of the rectangle in meters. What is the width of the rectangle if its area is 300 m2?

Answer 1

The equation for the area of the rectangle is given by:

A=40w - w²

But the value of the area A = 300

Substitute the value of A into the equation

300= 40w - w²

Rearrange the equation

w² - 40w + 300 = 0

The above is now a quadratic equation

To find the width, simply solve for w in the above quadratic equation.

Using the formula method to solve the above quadratic equation;

`w=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

w² - 40w + 300 = 0

a=1 b=-40 and c=300

substitute the values into the formula and evaluate

`w=\frac{-(-40)\pm\sqrt[]{(-40)^2-4(1)(300)}}{2(1)}`
`=\frac{40\pm\sqrt[]{1600-1200}}{2}`
`=\frac{40\pm\sqrt[]{400}}{2}`
`=(40\pm20)/(2)`
`=(40)/(2)\pm(20)/(2)`
`=20\pm10`

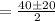
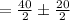
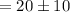
Either w = 20 + 10 or w= 20 - 10

w = 30 or w=10

This implies that there are two possible values for the width of the rectangle

Let's check our answer

p = 2l + 2w

80 = 2l + 2w

40 = l + w

If w = 30

l = 40 - 30 = 10

A = l x w = 10 x 30 = 300 m²

If w=10

l=40 - 10 = 30

A = l x w = 30 x 10 = 300 m²

Therefore, the width of the rectangle is either 30m or 10 m