We need to find a quadratic model from the news or social media.
We can model the number of people watching a story after t time of posting it.
When you post it, there are no people watching it, it starts at y=0. Throughout the day more people are watching, but when time passes, the number of people starts to decrease.
The situation can be modeled by the quadratic function:
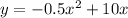
Where x is the time in hours after posting the story, and y is the number of new people who watched the story in the past hour.
If we graph the function it looks like this:
As can be seen, at the beginning the number of people watching the story starts to increase, but after some time the number of people you reach out to with your story starts to decrease until no one will watch it.
The quadratic term of the function is:
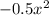
The coefficient of the quadratic term determines how wide or narrow the graphs are, and whether the graph turns upward or downward. As we have a negative coefficient, then the parabola opens down.
The linear term is 10x, and it determines the position of the vertex.
There is a maximum value and it occurs at t=10 when you reach out to 50 people: (10,50).
The domain of the function is the set of possible x-values, as can be seen in the graph, it is [0,20], which means after 20 hours no one will watch your story.
The range is the set of y-values the function takes. It is [0,50]. It means you start with 0 people and the maximum number of people you reach out to in one hour is 50.