Question

In a race between 18 people, how many ways can the top 5 finishers be arranged? 1) 1,028,1602) 8,5683) 742,5604) 73,440

Answer 1

Given:

Number of people, n = 18

Let's determine the number of ways the top 5 finishers can be arranged.

Here, we are to use the permutation formula.

Apply the formula:

`^nP_r=(n!)/((n-r)!)`

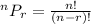
Where:

n = 18

r = 5

Thus, we have:

`\begin{gathered} ^(18)P_5=(18!)/((18-5)!) \\ \\ ^(18)P_5=(18!)/((13)!) \end{gathered}`

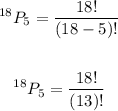
Solving further:

`\begin{gathered} ^(18)P_5=(18\ast17\ast16\ast15\ast14\ast13!)/(13!) \\ \\ ^(18)P_5=18\ast17\ast16\ast15\ast14 \\ \\ ^(18)P_5=1028160 \end{gathered}`

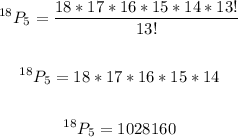
Therefore, there are 1,028,160 ways in which the top 5 finishers can be arranged.

ANSWER:

1) 1,028,160