Given that the membership fee of $20 is constant, the amount of video rented is $2.50 per video.
It can be observed that the independent variable is the number of video rented at the rate of $2.50, which can also be regarded as the gradient. The membership fee is constant, while the revenue is the dependent variable that is determine based on varied number of video rented.
This information can modelled using the linear equation below

The graph of the modelled linear equation is as shown below
Hence, the linear equaton modelled is y = 2.5x + 20 and the graph is as shown above
2) If 5 videos are rented, the revenue is as calculated below:
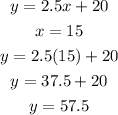
Hence, the revenue when 15 videos were rented is $57.50
3) If a new member paid the store $67.50 in the last 3 months, the number of video rented would be
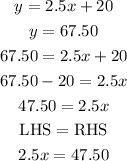
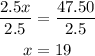
Hence, the number of videos rented when a new member paid $67.50 is 19