Question

One woman won $1 million from the lottery. Years later she won $1million again. In the first game she beat the odds of 1 in 5.2 million to win. In the second she beat odds of 1 in 805,600.

Answer 1

Given that:

Amount win from the scratch-off game = $1 million

The individual beat odds of 1 in 6.2 million to win in the first game and in the second game, the individual beat odds of 1 in 805600.

Let A and B denote the events "Won in first game" and "Won in the second game".

Then, find P(A) and P(B)5

`\begin{gathered} P(A)=\frac{1}{5.2\text{ Million}} \\ =(1)/(5.2*10^6) \\ =1.92*10^(-7) \end{gathered}`
`\begin{gathered} P(B)=(1)/(805600) \\ =1.24*10^(-6) \end{gathered}`

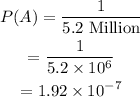
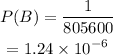
(a) P(Indiviual win in both games)

`\begin{gathered} =P(A)* P(B) \\ =1.92*10^(-7)*1.24*10^(-6) \\ =2.381*10^(-13) \end{gathered}`

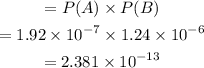
(b) P(Individual win twice in the second game)

`\begin{gathered} =P(B)* P(B) \\ =1.24*10^(-6)*1.24*10^(-6) \\ =1.54*10^(-12) \end{gathered}`