Question

An off roader explores the open desert in her Hummer. First she drives 25 degrees west of north with a speed of 6.5km/h for 15 mins then due east with a speed of 12km/h for 7.5mins. She completes the final leg of her trip in 22mins. What is the direction and speed of travel of the final leg. (Assume her speed is constant on each leg and that she returns to her starting point at the end of the final leg).

Answer 1

She completes the final leg with a speed of 4.58 km/h and travels 61.15 degrees south of the west.

Step-by-step explanation:

Let's calculate the distance traveled on each leg.

First, she drives 6.5 km/h for 15 min in a direction of 25 degrees west of north, so the distance traveled is:

Then, she drives due east at a speed of 12km/h for 7.5min, so the distance traveled is:

Now, we can represent the situation using the following figure:

So, we need to find the length of the red segment and its direction.

First, let's find the value of angle θ, so it will be equal to:

θ = 180 - 90 - 25 = 65

Because the interior angles of the formed triangle with the green line sum 180 and one of the angles is 25 and the other is 90 degrees.

Now, we can use the cosine rule to find the red leg as follows:

`\begin{gathered} c^2=a^2+b^2-2ab\cos (\theta) \\ c^2=1.625^2+1.5^2-2(1.625)(1.5)\cos 65 \\ c^2=2.83 \\ c=\sqrt[]{2.83}=1.68\text{ km} \end{gathered}`

Because a and b are the lengths of the known legs and c is the length of the final leg.

Finally, we can use the same rule to find the angle α, so we get:

`\begin{gathered} a^2=b^2+c^2-2bc\cos (\alpha) \\ a^2-b^2-c^2=-2bc\cos (\alpha) \\ \cos (\alpha)=(a^2-b^2-c^2)/(-2bc) \end{gathered}`

Replacing the values, we get:

`\begin{gathered} \cos \alpha=(1.625^2-1.5^2-1.68^2)/(-2(1.5)(1.68)) \\ \cos \alpha=0.4825 \\ \alpha=\cos ^(-1)(0.4825) \\ \alpha=61.15 \end{gathered}`

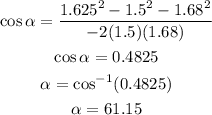
Now, we can calculate the speed of travel of the final leg as:

`\begin{gathered} t=22\min *(1h)/(60\min )=0.367\text{ h} \\ v=(d_c)/(t)=\frac{1.68\text{ km}}{0.367h}=4.58\text{ km/h} \end{gathered}`

Therefore, the answers are:

She completes the final leg with a speed of 4.58 km/h and travels 61.15 degrees south of the west.