Question

5. The aspect ratio (the ratio of screen width to height) of arectangular flat-screen television is 16:9. The length of the diagonalof the screen is the television's screen size. Determine and state, thethe nearest tenth of an inch, the screen size (diagonal) of this flat-screen television with a screen height of 22.3 inches.

Answer 1

`45.5in`

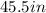
1) In this problem, we're dealing with ratios and then we can write out the following:

`16:9\Rightarrow(16)/(9)`

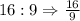
2) Since the screen height is 22.3 and the aspect ratio we can write out the following proportion:

`\begin{gathered} (16)/(9)=(x)/(22.3) \\ 9x=16*22.3 \\ 9x=356.8 \\ (9x)/(9)=(356.8)/(9) \\ x=39.64 \end{gathered}`

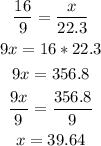
3) Note that we need to consider a right triangle, in which the hypotenuse is the diagonal so we can write ou the following:

`\begin{gathered} a^2=b^2+c^2 \\ a^2=\left(39.64\right)^2+\left(22.3\right)^2^ \\ a^=√(\left(39.64\right)^2+\left(22.3\right)^2) \\ a=45.48 \end{gathered}`

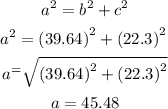
Note that we used the Pythagorean relation.