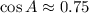ANSWER
cos A = √20/6 ≈ 0.75
Step-by-step explanation
Triangle ABC is:
Since this is a right triangle we can use the trigonometric ratios to find cosA:
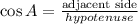
the hypotenuse of this triangle is side c, and the adjacent side is side b. We don't have side b, but we have two sides and again, as this is a right triangle, we can use the Pythagorean theorem to find the missing side:
![\begin{gathered} c^2=a^2+b^2 \\ b=\sqrt[]{c^2-a^2} \\ b=\sqrt[]{6^2-4^2} \\ b=\sqrt[]{36-16} \\ b=\sqrt[]{20} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/5ul35tu9155u2nix70kdws7911lucuhv12.png)
The cosine of A is then:
![\cos A=(b)/(c)=\frac{\sqrt[]{20}}{6}](https://img.qammunity.org/2023/formulas/mathematics/college/2vyencpyf1op3za68v19wesobgn110mhns.png)
Rounded to the nearest hundredth: