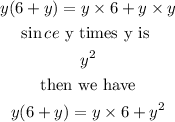Question

write an expression that is equivalent to each original expression use expressions in the box below not all Expressions will be used

Answer 1

The first expression is

`(7*6)+(7* y)`

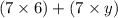
since there is 7 in both parenthesis, we can factorize 7, then we can write

`(7*6)+(7* y)=7(6+y)`

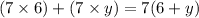
Second expression.

In this part, we have

`y(6+7)`

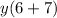
by applying the distributive law, this expression is equivalent to

`y(6+7)=y*6+y*7`

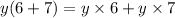
Third expression.

We have in this part:

`(6* y)+(6*7)`

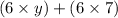
similarly to the first question, we can factorize 6, then we obtain

`(6* y)+(6*7)=6(y+7)`

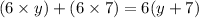
Fourth expression.

We have in this part:

`y(6+y)`

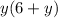
by applying the distributive law, this expression is equivalent to

`\begin{gathered} y(6+y)=y*6+y* y \\ \sin ce\text{ y times y is } \\ y^2 \\ \text{then we have} \\ y(6+y)=y*6+y^2 \end{gathered}`