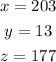For the given question, let the numbers are = x, y, and z
The sum of three integers is 393 ⇒ x + y + z = 393
The sum of the first and second integers exceeds the third by 39
so, x + y - z = 39
The third integer is 26 less than the first.
So, x - 26 = z
So, we have the following system of equations:
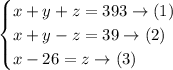
Substitute with (z) from equation (3) into equation (2):
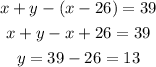
substitute with (y) into the equations (1) and (2)
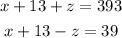
Add the equations to eliminate (z) then solve for (x):
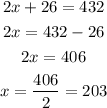
substitute with (x) into equation (3) to find (z)

so, the answer will be: