Question

the sum of two number is 45 and the difference is 17. what are the numbers?larger numbersmaller number

Answer 1

The Solution:

Let the two numbers be x and y.

The sum of the two numbers is 45.

`x+y=45\ldots\text{eqn}(1)`

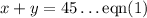
Their difference is 17.

`x-y=17\ldots\text{eqn}(2)`

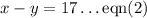
Solving the eqn(1) and eqn(2) by adding both equations together, we get

`2x=62`

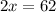
Dividing both sides by 2, we get

`x=(62)/(2)=31`

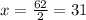
Substituting 31 for x in eqn(1), we get

`\begin{gathered} x+y=45 \\ 31+y=45 \\ \text{ Subtracting 31 from both sides, we get} \\ y=45-31 \\ y=14 \end{gathered}`

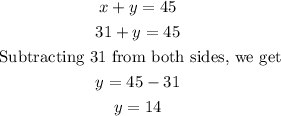
Therefore, the correct answer is:

Larger number = 31

Smaller number = 14