Question

You have two copper disks of same mass; disk 1 has twice the radius of disk 2. What is the ratio of the moment of inertia I 1 /I 2 ? (moment of inertia of a disk I= 1 /2 MR^ 2 )

Answer 1

`(I_(1))/(I_(2))=4`

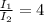
Step-by-step explanation

Let the mass of disks 1 and 2 be m.

Let the radius of disk 2 be R.

This implies that the radius of disk 1 is 2R.

The moment of inertia of disk 1 is given by:

`\begin{gathered} I_1=(1)/(2)m(2R)^2 \\ I_1=(1)/(2)m*4R^2 \\ I_1=2mR^2 \end{gathered}`

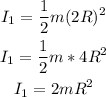
The moment of inertia of disk 2 is given by:

`I_2=(1)/(2)mR^2`

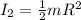
Therefore, the ratio of the moment of inertia of disk 1 to disk 2 is:

`\begin{gathered} (I_1)/(I_2)=(2mR^2)/((1)/(2)mR^2) \\ (I_1)/(I_2)=(2)/((1)/(2))=2*2 \\ (I_1)/(I_2)=4 \end{gathered}`

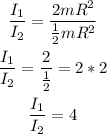
That is the answer.