Question

I need answer please​

Answer 1

Answer: Choice C

No, because the product of the slopes is not -1.

===================================================

Step-by-step explanation:

Let's find the slope of line DE.

`D = (x_1,y_1) = (1,-2) \text{ and } E = (x_2,y_2) = (3,4)\\\\m = (y_(2) - y_(1))/(x_(2) - x_(1))\\\\m = (4 - (-2))/(3 - 1)\\\\m = (4 + 2)/(3 - 1)\\\\m = (6)/(2)\\\\m = 3\\\\`

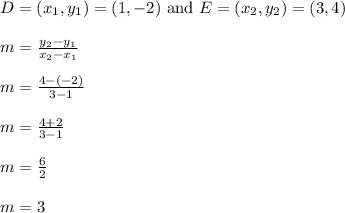
The slope of line DE is 3.

-----------------

Use similar steps to find the slope of line FG.

`F = (x_1,y_1) = (-1,2) \text{ and } G = (x_2,y_2) = (4,0)\\\\m = (y_(2) - y_(1))/(x_(2) - x_(1))\\\\m = (0 - 2)/(4 - (-1))\\\\m = (0 - 2)/(4 + 1)\\\\m = -(2)/(5)\\\\`

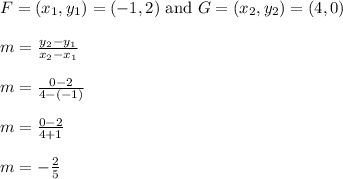
Line FG has a slope of -2/5

-----------------

Now multiply the two slopes together

3*(-2/5) = -6/5 = -1.2

The product of the slopes is not -1, so the lines are not perpendicular.

This confirms why choice C is the answer.